고차 다항식 보간에서 가장 흔히 발생하는 문제 중 하나가 Runge 현상 (Runge's Phenomenon)입니다. 이는 보간 과정에서 발생하는 수치적 불안정성으로, 특히 균등한 간격으로 노드를 배치했을 때 더욱 두드러집니다.
1. Runge 현상이란?
Runge 현상은 고차 다항식을 사용하여 함수 보간을 수행할 때, 보간 다항식이 구간의 양 끝에서 과도하게 진동하는 문제를 의미합니다. 이 현상은 1901년 독일의 수학자 Carl Runge가 연구한 결과에서 처음 보고되었습니다. Carl Runge는 1901년에 발표한 연구에서
$$
f(x) = \frac{1}{1+25x^2}
$$
함수를 균등하게 분포된 노드에서 보간할 경우, 노드의 수가 증가함에 따라 경계 근처에서 큰 진동이 발생한다는 사실을 관찰했습니다. 이 결과는 이후 수치해석 및 보간 이론의 교과서들(예: Burden & Faires의 Numerical Analysis)에서 인용되며, 고차 다항식 보간의 한계를 설명하는 대표적인 사례로 자리잡고 있습니다.
Runge는 위 함수를 $[-1,1]$ 구간에서 균등하게 배치된 $n+1$개의 노드로 보간할 때, 노드 수가 증가함에 따라 보간 다항식이 원래 함수와 크게 차이나며, 특히 구간의 양 끝에서 오차가 급격히 증가하는 현상을 발견했습니다. 이러한 진동은 다항식의 차수가 증가할수록 더 심해지며, 심지어 무한 차수의 다항식을 사용해도 원래 함수로 수렴하지 않는 경우가 발생합니다.

2. Runge 현상의 원인
Runge 현상의 주요 원인은 다항식 보간의 기저 함수 (Lagrange 기저 함수)가 구간의 양 끝에서 급격히 커지는 성질에 있습니다. 균등 분포된 노드를 사용할 경우, 높은 차수의 보간 다항식은 중심부에서는 원래 함수와 잘 맞으나, 경계 근처에서는 극단적인 진동(overshooting)이 발생하기 쉽습니다.
이러한 현상은 두 가지 요인에 기인합니다.
- Lagrange 기저 함수의 성질:
고차 다항식을 사용하면, 각 Lagrange 기저 함수가 구간의 양 끝에서 매우 높은 값을 가지게 됩니다. 이로 인해 작은 오차라도 경계에서 증폭되어 전체 보간 다항식의 진동을 유발합니다. - 다항식의 수렴 한계:
Weierstrass 근사 정리에 따르면, 임의의 연속 함수 $f$는 유계 폐구간 $[a, b]$에서 다항식으로 임의로 근사될 수 있습니다.
Weierstrass 근사 정리 (Weierstrass Approximation Theorem):
임의의 연속 함수 $f$가 $[a, b]$에서 주어졌을 때, 임의의 양수 $\varepsilon > 0$에 대해
$$
|f(x) - p(x)| < \varepsilon \quad \text{for all } x \in [a, b]
$$
를 만족하는 다항식 $p$가 존재한다는 정리입니다.
그러나 실제 보간 문제에서는 균등한 노드 분포가 다항식의 수렴에 방해가 될 수 있습니다.
3. Runge 현상 완화 방법
Runge 현상을 완화하기 위한 주요 전략은 비균등한 노드 배치입니다. 대표적으로 Chebyshev 노드와 Gauss–Lobatto 노드가 사용됩니다.
✅ Chebyshev 노드
- 정의: Chebyshev 다항식의 근을 노드로 사용합니다.
- 특징: 노드들이 구간의 끝으로 갈수록 촘촘하게 배치되어, 경계 근처의 진동(overshooting)을 줄입니다.
- 수식: 주어진 구간 $[-1,1]$에서 $n+1$개의 Chebyshev 노드는
$$
x_i = \cos\left(\frac{(2i+1)\pi}{2(n+1)}\right), \quad i = 0, 1, \dots, n
$$
로 정의됩니다.
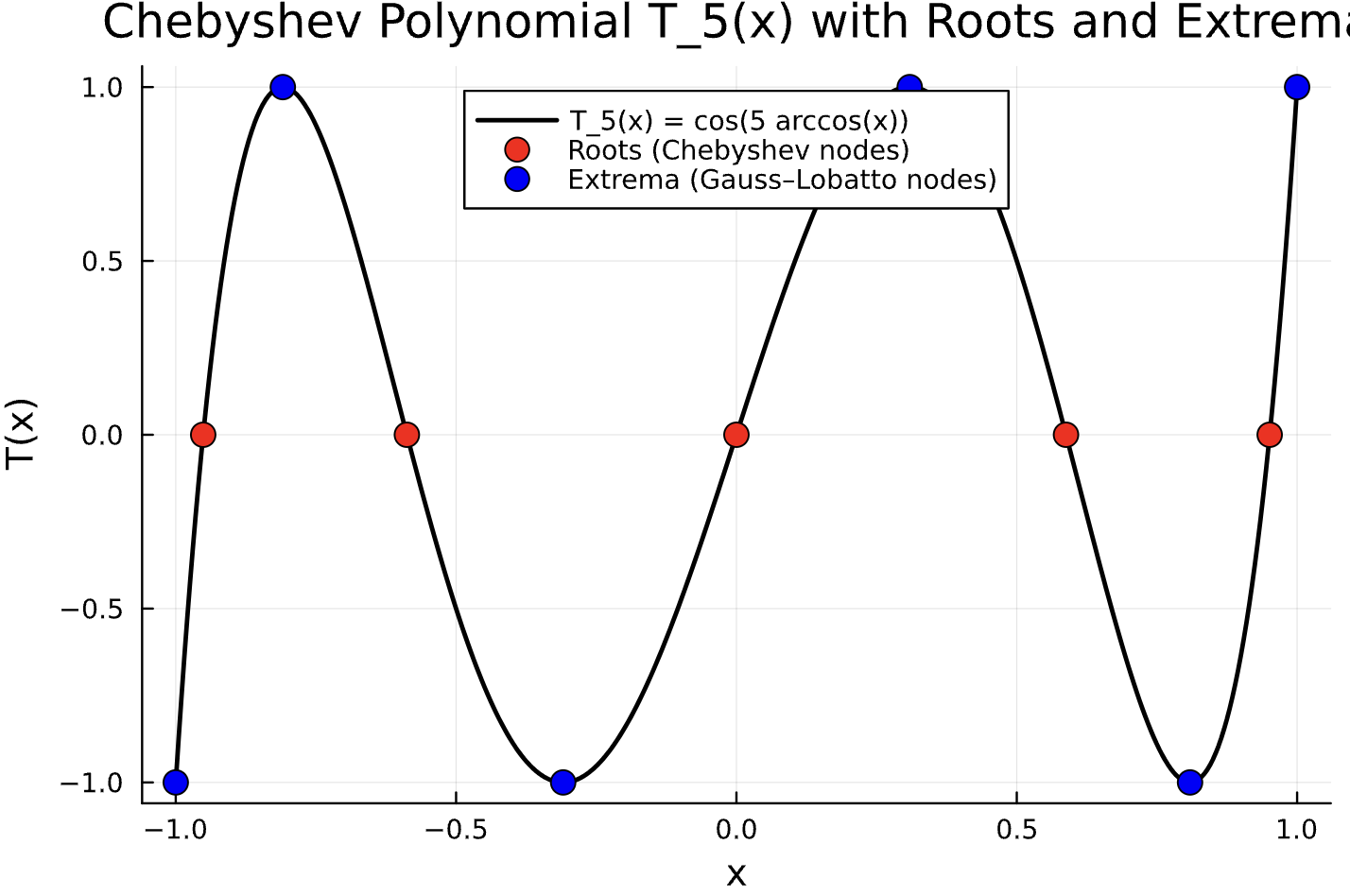
✅ Gauss–Lobatto 노드 (Chebyshev–Lobatto 노드)
- 정의: Chebyshev 다항식의 극점(extrema)을 노드로 사용하며, 구간의 양 끝점($-1$과 $1$)을 포함합니다.
- 특징: 경계 조건이 중요한 문제에서 유리하며, 레베그 상수를 낮춰 보간의 안정성을 향상시킵니다.
- 수식: $[-1,1]$ 구간에서 $n+1$개의 Gauss–Lobatto 노드는
$$
x_i = \cos\left(\frac{\pi i}{n}\right), \quad i = 0, 1, \dots, n
$$
로 정의됩니다.
이러한 비균등 노드들은 보간 다항식의 레베그 상수 (Lebesgue constant) 를 낮추는 효과가 있습니다.
레베그 상수란?
레베그 상수는 보간 과정에서 원래 함수와 보간 다항식 사이의 오차가 얼마나 증폭될 수 있는지를 나타내는 척도입니다.
주어진 노드 ${x_i}$와 해당 Lagrange 기저 다항식 $L_i(x)$에 대해, 레베그 상수는
$$
\Lambda_n = \max_{x \in [a,b]} \sum_{i=0}^{n} |L_i(x)|
$$
로 정의됩니다. 이 값이 작을수록 보간 과정에서의 오차 증폭이 줄어들어 보다 안정적인 결과를 얻을 수 있습니다.

4. Runge 현상과 Gauss–Lobatto 노드의 역할
Gauss–Lobatto 노드는 균등 노드를 사용할 때보다 여러 면에서 유리합니다.
- 경계에서의 안정성
Gauss–Lobatto 노드는 구간의 양 끝점을 포함하므로, 경계 조건을 엄격히 반영할 수 있습니다. 이 특성은 불연속 갤러킨(dG) 방법이나 유한 요소법(FEM)에서 매우 중요하게 작용합니다. - Runge 현상 완화
균등 노드의 경우, 전 구간에 걸쳐 보간 다항식의 차수가 증가하면 경계 근처에서 오차가 증폭되는 Runge 현상이 나타납니다.
반면, Gauss–Lobatto 노드는 경계에서 더 밀집된 노드 분포를 제공하므로 글로벌 보간에서도 오차 증폭이 덜 발생합니다.- 전 구간(global) 보간에서 균등 노드를 사용하면, 노드 수를 늘리더라도 다항식 차수가 계속 증가하면서 경계 근처의 오차가 크게 증폭됩니다.
- 실제 물리 시뮬레이션에서는 전체 영역을 작은 요소로 분할하여 각 요소 내에서 저차 다항식 보간(예: 스플라인 보간이나 FEM)을 사용하면, 각 요소 내 노드가 밀집되어 오차를 효과적으로 제어할 수 있습니다.
- 그러나 글로벌 보간의 경우 단순히 mesh width가 줄어드는 것만으로는 Runge 현상을 해결하기 어렵고, 노드 분포를 비균등하게 선택하는 전략이 필요합니다.
- 수치적분 정확도 향상
Gauss–Lobatto 구적법은 Newton–Cotes 방식보다 더 최적화된 노드 분포를 사용하여, 동일한 노드 수에서 더 높은 다항식 차수를 정확하게 적분할 수 있습니다.- Newton–Cotes 방식:
균등 노드를 사용하므로, 저차 다항식에 대해서는 양호한 정확도를 보이나 고차 다항식에서는 오차가 커지고 불안정해질 수 있습니다. 특히 폐 Newton–Cotes 공식의 경우, $n+1$개의 노드로 다항식 차수가 최대 $n$까지 정확하게 적분될 수 있으나, 고차에서는 오차와 진동 문제가 발생할 수 있습니다. - Gauss–Lobatto 방식:
경계점을 포함하는 비균등 노드를 사용하여 동일한 노드 수 내에서 보통 $2n-3$ 차 다항식까지 정확하게 적분할 수 있습니다. 또한, 최적화된 노드 선택으로 인해 레베그 상수 측면에서도 우수하여 전반적인 오차와 불안정성이 낮습니다.
- Newton–Cotes 방식:

5. 결론
Runge 현상은 고차 다항식 보간에서 균등한 노드 배치로 인해 발생하는 진동 문제입니다. 이를 해결하기 위해, 비균등한 노드 배치 (Chebyshev 또는 Gauss–Lobatto 노드 사용) 가 효과적인 전략으로 활용됩니다.
특히, Gauss–Lobatto 노드는 경계 조건의 엄격한 반영, Runge 현상 완화, 그리고 높은 수치적분 정확도 등의 장점을 제공하므로, 불연속 갤러킨 (dG) 방법이나 유한 요소법(FEM)과 같은 고차 수치 근사 기법에서 널리 사용됩니다.
✅ 정리하면, Runge 현상을 방지하기 위해 Gauss–Lobatto 노드를 사용하는 것이 효과적인 선택이며, 이는 수치해석에서 고차 다항식 근사를 안정적으로 수행하는 데 중요한 역할을 합니다!